4.치환 행렬(Permutation), 소거 행렬(Elimination)

치환 행렬 P

치환 행렬(permutation matrix)란 말그대로 행렬의 행 또는 열을 교환하는 행렬을 말한다. 치환 행렬의 특수한 경우로 항등 행렬이 있다. 이해를 쉽게 하기 위해 항등 행렬로 부터 시작하려 한다.

$$ I = \begin{bmatrix}1 & 0 \\ 0 & 1 \end{bmatrix}\, , \, \begin{bmatrix}1 & 0 &0 \\ 0 & 1 &0 \\ 0 & 0 & 1 \end{bmatrix} $$

치환 행렬은 “P”로써 표현한다.
치환 행렬 P는 각 행과 열에 정확히 하나의 1이 들어가며, 그 결과 행/열 벡터가 선형 독립이어서 가역적이다.
치환 행렬 P의 역행렬은 P의 전치행렬(Transpose)과 같다.

$$ P^{-1} = P^{T}\, , \, P^{T}P = I $$

행 관점의 행렬곱으로 바라보면 다음과 같다.

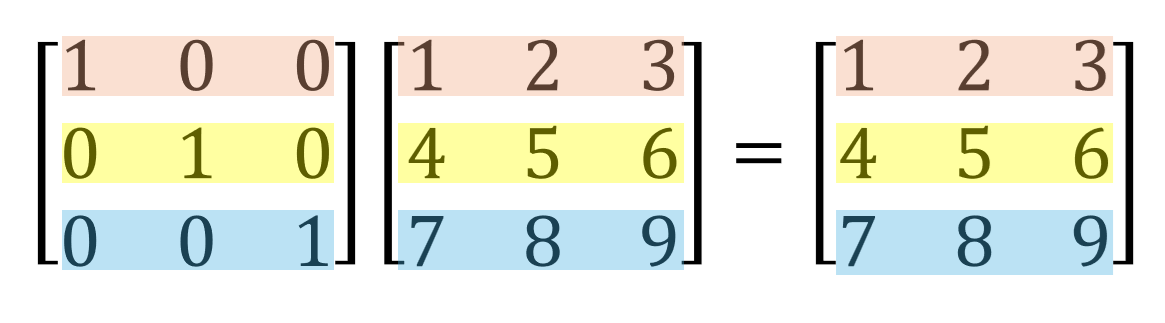
그림 1. 행 관점으로 보는 치환 행렬(항등 행렬)과 행렬

• \((1,0,0)^{T}\)는 첫 번째 행렬 \((1,2,3)^{T}\)만 선택한다.
• \((0,1,0)^{T}\)는 두 번째 행렬 \((4,5,6)^{T}\)만 선택한다.
• \((0,0,1)^{T}\)는 세 번째 행렬 \((7,8,9)^{T}\)만 선택한다.

따라서 \(IA = A\)가 나오는 것이다.

이는 열관점으로 봐도 같다.

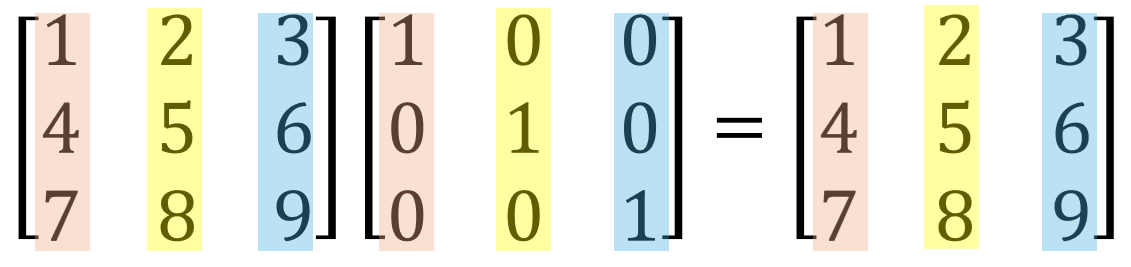
그림 2. 열 관점으로 보는 치환 행렬(항등 행렬)과 행렬

• \((1,0,0)\)는 첫 번째 행렬 \((1,4,7)\)만 선택한다.
• \((0,1,0)\)는 두 번째 행렬 \((2,5,8)\)만 선택한다.
• \((0,0,1)\)는 세 번째 행렬 \((3,6,9)\)만 선택한다.

이를 바탕으로 행 혹은 열을 바꾸고 싶다면, 원하는 행, 열이 선택되도록 치환 행렬을 만들면 된다.

$$ \begin{bmatrix}1 & 0 &0 \\ 0 & 0 &1 \\ 0 & 1 & 0 \end{bmatrix}\begin{bmatrix}1 & 2 &3 \\ 4 & 5 &6 \\ 7 & 8 & 9 \end{bmatrix} \quad = \quad \begin{bmatrix}1 & 2 &3 \\ 7 & 8 &9 \\ 4 & 5 & 6 \end{bmatrix} $$

소거 행렬 E

\(Ax = b\)를 풀 때, 소거법을 이용해서 문제를 풀었다. 소거법을 표현하기 위해 “1행을 3배해서 2행에 뺀다.”등의 구체적으로 적어 표현을 하였는데, 이를 수학적으로 표현 하기 위해 소거 행렬 E를 사용한다.

$$ \begin{aligned} &\! Ax\quad=\quad b \\[8pt] &\! EA\quad = \quad U \\[8pt] \end{aligned}

\(U\)는 A를 소거법을 적용했을 때 나오는 상삼각 행렬이다.

우리가 사용할 소거 행렬은 구체적으로 다음과 같이 표시한다.

$$ \begin{aligned} &\! E_{mn} = m행의\, n번째\,원소를\,없애기\,위해\,n행을\,적절히\,배수해\,m행에\,더하는\,행렬 \\[8pt] &\! E_{32}E_{31}E_{21}A\quad = \quad U \\[8pt] \end{aligned} $$

소거 행렬을 다루기 위해서는 행렬들 간의 덧셈, 뺄셈을 표현하는 것이 필요하다.
3 by 3 행렬을 통해 알아보자.

첫 번째 행에 m을 곱해서 두 번째 행에 뺀다고 해보자. 그러면 다음과 같이 표현한다.

$$ \begin{bmatrix}1 & 0 &0 \\ -m & 1 &0 \\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix}1 & 2 &3 \\ 4 & 5 &6 \\ 7 & 8 & 9 \end{bmatrix} $$

행의 관점으로 보자.

• \((1,0,0)^{T}\, , \, (0,0,1)^{T}\)의 경우 항등 행렬이라 \((1,2,3)^{T}\, , \, (7,8,9)^{T}\)가 그대로 나온다.
• \((-m,1,0)^{T}\)의 경우 가운데 1은 항등 행렬의 일부분으로써 \((4,5,6)^{T}\)가 나오지만, -m의 경우 첫번째 항에 곱해져 나온다.

따라서 결론적으로 식의 결과는 첫 번째 항에 m을 곱해 두 번째 항에 뺀 결과가 된다.

다음 2가지의 경우를 더 알아보자?

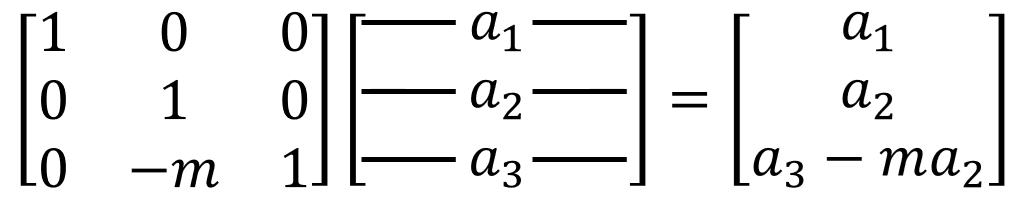
그림 3. $$E_{32}$$의 경우

이 경우는 세 번째 항이 두 번째 항에 m을 곱해서 세 번째 항에 뺸 값이 된다.

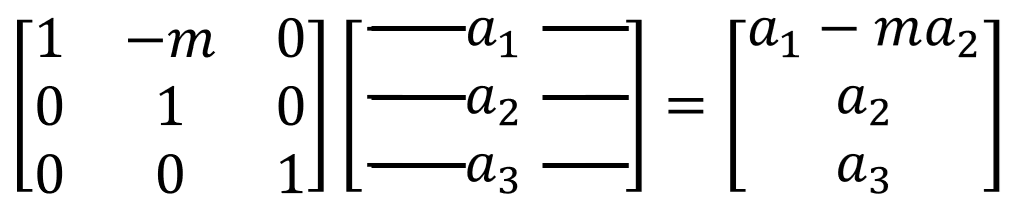
그림 4. 대각 요소 위에 있는 경우 (row)

이 경우는 반대로 두 번째 항에 m을 곱해서 첫 번째 항에 뺀 값이 결과가 된다.
열 계산은 행 계산과 비슷 하다.

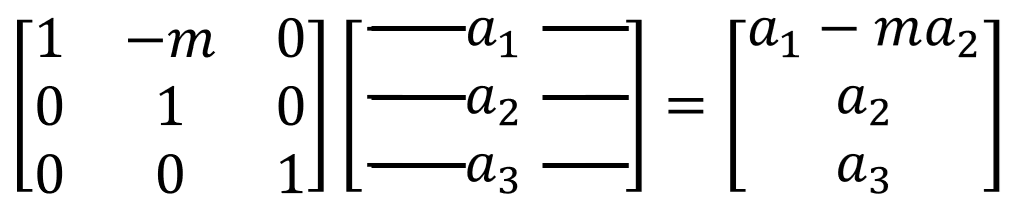
그림 5. 열 계산

다만 행 계산에서는 대각 요소 아래에 두어야 그자리에 계산이 되었던것이, 열 계산에서는 대각 요소 위에 두어야 한다. 따라서 열 계산에서는 대각 요소 아래에 두게 되면 반대로 계산이 된다. 행 연산은 왼쪽에서 적용이 되고, 열 연산은 오른쪽에서 적용되기 때문이라고 이해하면 편하다.

마지막으로 \(E_{32}E_{31}E_{21}A\)를 \(EA\)(\(E\)는 소거행렬들을 곱한 하나의 행렬)로 줄일 수 있을까? 할수 있다.

$$ \begin{aligned} &\!\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -k & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -n & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ -m & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\\[14pt] &\! = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -k & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 \\ -m & 1 & 0 \\ -n & 0 & 1 \end{bmatrix}\\[14pt] &\! =\begin{bmatrix} 1 & 0 & 0 \\ -m & 1 & 0 \\ km -n & -k & 1 \end{bmatrix} \end{aligned} $$

참고 자료

• Gilbert Strang, MIT 18.06 Linear Algebra, MIT OCW 강의 (2011)