3.Matrix multiplication(행렬곱)

행렬곱

우리는 \(Ax=b\)를 열 관점(Column picture) 벡터들의 선형결합으로 바라보고, 행 관점(Row picture)으로 직선들의 교점으로써 바라봤다. 이 처럼 행렬의 곱셈 또한 여러가지 관점으로 볼 수 있다.

• Row \(\times\) Column
• Columns
• Rows
• Column \(\times\) Row
• Block

Row \(\times\) Column

가장 먼저 우리가 학교에서 배우는 행과 열의 곱으로써 바라보는 방법이다. 행렬 A(m by n)와 행렬 B(n by l)를 곱해 행렬 C(m by l)를 얻는다고 할 때, 곱해지는 왼쪽의 행렬의 열과 오른쪽 행렬의 행의 크기가 같아야 계산이 이루어 진다.

$$ \begin{bmatrix}a_{11} & a_{12} \\a_{21} & a_{22} \end{bmatrix}\begin{bmatrix} b_{11} \\b_{21} \end{bmatrix} \quad = \quad \begin{bmatrix}c_{11}\\c_{21} \end{bmatrix} $$

위와 같은 식이 있다고 할 때, 계산 방법은 다음과 같다.

$$ \quad C_{ij} = \sum\limits_{k=1}^n a_{ik}b_{kj}\quad \quad (n은\,행렬\,A의\,열의\,크기) $$

단순하지만, 빠르게 계산 할 수 있다.

Columns

열 관점으로 계산하는 것은 간단하다.

행렬 A와 행렬 B를 곱해서 행렬 C를 얻는다고 할때, 행렬 A와 행렬 B의 j 열을 곱한 값은 행렬 C의 j열이다.

즉, C의 j열은 B의 j열의 원소들을 계수로 하는 A 열들의 선형 결합이다.

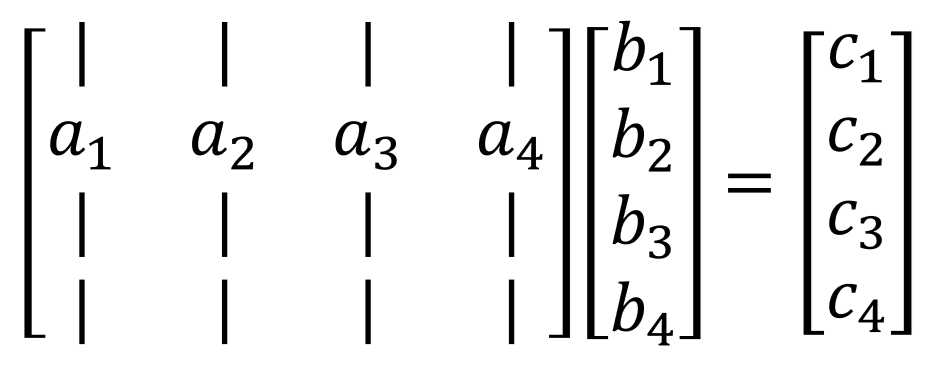
그림 1. 풀어야하는 식

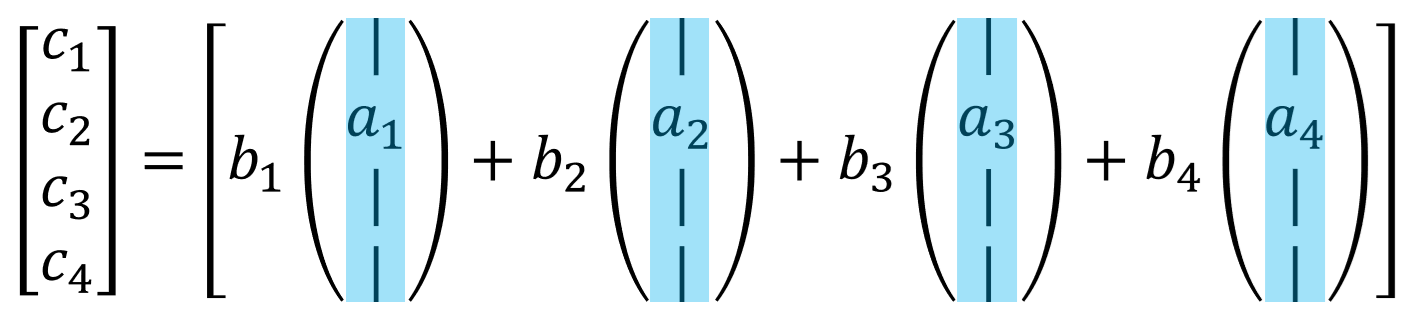
그림 2. A의 선형결합으로 이루어진 곱셈 결과

C의 j열은 B의 j열이 관여 한다는 점이 중요하다. 2가지 예시를 통해 알아보자.

$$ \begin{bmatrix}1 & 1 &0 \\ 0 & 1 & 1 \\ 1&0&1 \end{bmatrix}\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} $$

이 경우에는 B가 벡터이다. 따라서 C가 B의 원소를 계수로 A열 벡터들의 선형결합으로 나오게 된다.

$$ 1\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix} + 2\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} + 3\begin{bmatrix} 0 \\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 3 \\ 5 \\ 4 \end{bmatrix} $$

그다음 경우를 보자

$$ \begin{bmatrix}1 & 1 &0 \\ 0 & 1 & 1 \\ 1&0&1 \end{bmatrix}\begin{bmatrix} 1 &2&3\\ 2 &4 &6\\ 3&6&9 \end{bmatrix} $$

이 경우에는 B가 행렬이고, C 또한 행렬로 나오게 된다. 하지만 B를 벡터들의 집합 느낌으로 보게 된다면, B의 벡터가 C의 각 벡터에 영향을 주어 답이 나온 것을 알 수 있다.

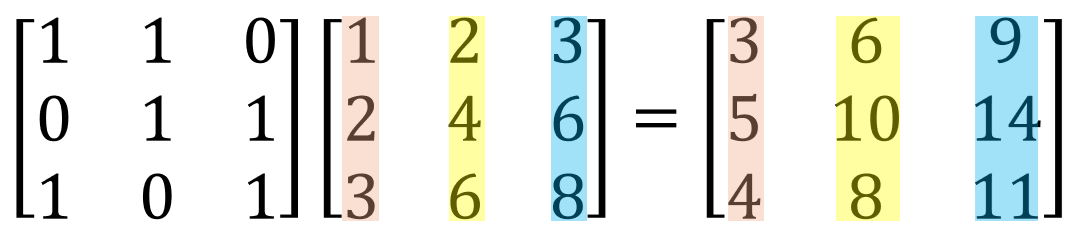
그림 3. B가 C의 각각의 열에 선형결합으로 이루어진 곱셈 결과

Rows

행 관점은 열과 비슷 하다.

행렬 A의 i번째 행과 행렬 B를 곱한 값은 행렬 C의 i번째 행이다.

즉, C의 i번째 행렬은 A의 i번째 행의 원소들을 계수로 하는 B의 선형 결합이다.

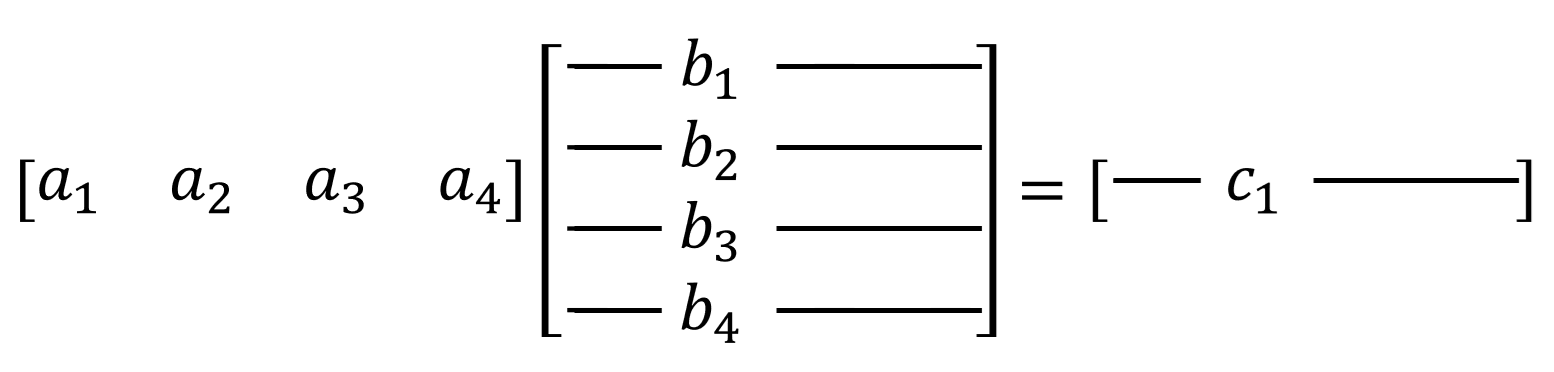
그림 4. 풀어야하는 식2

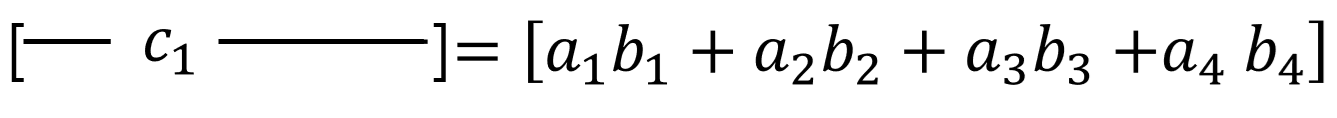
그림 5. B의 선형결합으로 이루어진 결과 값

행 관점에서도 A가 행렬이여도 벡터들의 집합으로 바라볼 수 있다.

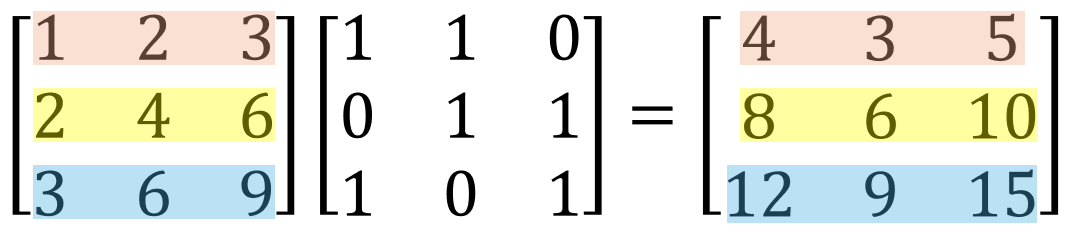
그림 6. 행관점으로 보는 계산 예시

여기서 알아야 할점이 열 관점이나 행 관점이나 결과 값이 그에 맞는 벡터로 나온다는 것이다.
열 벡터를 행렬에 곱할 경우 똑같은 열 벡터가 나오고 행 벡터를 행렬에 곱하면 행 벡터가 나온다.

이를 만족시키기 위해서는 열의 경우는 행렬의 오른쪽에 곱해져야 한다. 그리고 행의 경우는 행렬의 왼쪽에 곱해져야 한다. 오른쪽은 열의 영향을 주고, 왼쪽은 행에 영향을 준다고 생각하면 편하다.

Column \(\times\) Row (열 벡터 x 행 벡터)

그러면 반대는 어떻게 될까?

Column \(\times\) Row의 경우는 결과 값이 행렬로 나오게 된다.
이는 더 자세히 표현하면 ”벡터와 벡터의 곱이 행렬로 나온다.“ 라고 할 수 있다.

$$ \begin{bmatrix}2 \\3 \\4 \end{bmatrix}\begin{bmatrix} 1 & 6 \end{bmatrix} \quad = \quad \begin{bmatrix} 2 & 12 \\ 3 & 18\\ 4 & 24 \end{bmatrix} $$

조금 더 나아가면,열 로써 바라보자. 그러면 결과 값은 열 벡터인 (2, 3, 4)가 행 벡터 \((1, 6)^T\)의 원소들 만큼의 배로 각 열에 존재한다는 것을 알 수 있다.

행으로 바라봐도 마찬가지로, 결과 값은 행 벡터 \((1, 6)^T\)가 열 벡터 (2, 3, 4)의 원소 배로 각 행에 위치 한다는 것을 알 수 있다.

선형대수에서는 앞에서 말한 것 처럼 벡터 표현을 열벡터로 표현한다.

이러한 사실은 계산의 편의성 뿐만 아니라,각 열 혹은 행 벡터가 종속이라고도 표현할 수 있고, 좌표로 표현하면 같은 직선상에 놓여 있다고도 표현할 수 있다.

Block

마지막은 바로 예시를 통해 알아보자. 다음과 같은 식이 있다고 하자.

$$ \begin{bmatrix}1 & 0 & 1 & 0 \\0 & 1 & 0 & 1 \\1 & 0 & 1 & 0 \\0 & 1 & 0 & 1\end{bmatrix}\begin{bmatrix}2 \\3 \\2 \\3 \end{bmatrix}\quad = \quad\begin{bmatrix}c_{1} \\ c_{2} \\ c_{3} \\ c_{4}\end{bmatrix} $$

이 식은 2x2 블록으로 나눌수 있도록 패턴이 존재한다.

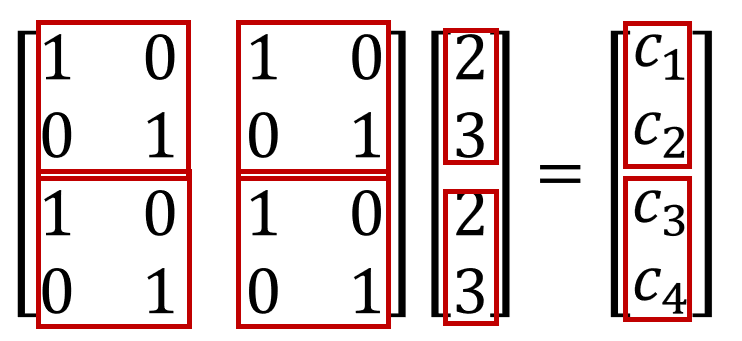
그림 7. 행렬을 블록으로 나누기

따라서 이를 블록으로 나누어 보면 다음과 같다.

$$ \begin{aligned} &\!\begin{bmatrix} A & A \\ A & A \end{bmatrix}\!\begin{bmatrix} B \\ B \end{bmatrix} = \begin{bmatrix} C \\ C \end{bmatrix} \\[14pt] &\!\begin{bmatrix} C \\ C \end{bmatrix} = \!\begin{bmatrix} 2AB \\ 2AB \end{bmatrix} \\[14pt] &AB = \!\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}\!\begin{bmatrix}2 \\ 3\end{bmatrix} = \!\begin{bmatrix}2 \\ 3\end{bmatrix} \\[14pt] &\!\begin{bmatrix} C \\ C \end{bmatrix} = \!\begin{bmatrix} 4 \\ 6 \\ 4 \\ 6 \end{bmatrix} \end{aligned} $$

블록을 하나의 원소처럼 취급해서 곱하고 더하게 되면 계산이 더 구조화 되고 깔끔해진다. 다만 주의 해야 할점은 곱해져야하는 블록들의 크기가 맞아야 한다. 블록 A와 B를 곱할때, A의 열의 개수와 B의 행의 크기가 맞아야지 블록끼리 곱셈이 될것이고, 더하는 것도 크기가 맞아야 한다.

참고 자료

• Gilbert Strang, MIT 18.06 Linear Algebra, MIT OCW 강의 (2011)