5.역행렬(Inverse matrix), LU 분해
Published:
역행렬(Inverse Matrix)
수학에서 역은 원래 상태로 되돌리는 역할을 한다.
행렬에서 역행렬은 행렬 A에 대해 \(A^{-1}\)를 곱했을 때, 항등 행렬 I가 되는 행렬을 말한다.
이때, 행렬의 왼쪽, 오른쪽 상관 없이 곱해도 항등 행렬이 만들어진다.
$$ AA^{-1}\, =\, A^{-1}A\, =\, I $$
역행렬 특징
역행렬은 n by n matrix이고, pivot의 개수가 n개 일때, 존재한다.(선형 독립인 정사각행렬 or 가역 행렬이라고도 한다)
역행렬은 유일하다.
만약 BA = I, CA = I 라면, C = B = \(A^{-1}\) 이다.- A가 가역적이라면(역행렬이 존재한다면) \(Ax = b\)에 역행렬을 곱해서 해를 구할 수 있다.
\begin{align} Ax & =b \\ AA^{-1}x & =A^{-1}b \\ x & =A^{-1}b \end{align}
- 행렬 A가 역행렬을 가지기 위해서는 \(Ax = 0\)에서 \(x\)가 0벡터일때만 역행렬이 존재한다. 만약 A가 역행렬이 존재한다고 가정하자, 그러면 아래식이 참이여야 한다.
\begin{align} Ax & =0 \\ AA^{-1}x & =A^{-1}0 \\ x & =0 \end{align}
만약 \(x\)가 0이 아닌 해가 존재한다면 가정이 틀린것이므로 역행렬이 존재 하지 않는다. 1번과 4번은 모두 역행렬 존재 조건인 선형 독립성을 설명하는 것이다. (이는 이후에 더 자세히 다룬다.)
- 대각 행렬의 역행렬은 대각요소들의 역이다.
\begin{align} A \,=\, \begin{bmatrix} a_{1} & 0 & 0 \\ 0 & a_{2} & 0 \\ 0 & 0 & a_{3} \end{bmatrix} \quad , \quad A^{-1} \,=\, \begin{bmatrix} \frac{1}{a_{1}} & 0 & 0 \\ 0 & \frac{1}{a_{2}} & 0 \\ 0 & 0 & \frac{1}{a_{3}} \end{bmatrix} \end{align}
- 행렬 곱의 역행렬은 reverse order(역순)을 갖는다.
$$ (AB)^{-1}\, = \, B^{-1}A^{-1} $$
역행렬 계산법
역행렬은 Gauss-Jordan Method를 사용하면 쉽게 구할 수 있다.
- 행렬 A와 I를 같이 쓴다.
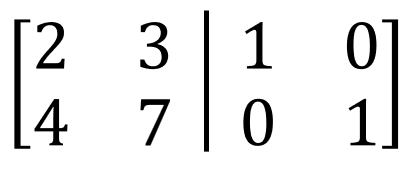
그림 1. 1단계 A와 I를 같이 쓴다. - 그 후 A를 I로 바꾼다. 그러면 I의 위치는 \(A^{-1}\)이 된다.

그림 2. A를 I로 바꾼다.(계산 과정)이는 \begin{align*} A &= I \, \text{가} \\ A^{-1}A &= A^{-1}I \, \text{가 되어} \\ I &= A^{-1} \, \text{가 된다고 생각하면 편하다.} \end{align*}
치환 행렬, 소거 행렬의 역행렬
치환 행렬 P의 경우 역행렬과 전치(transpose)행렬이 같다.
$$ P^{T}\, =\, P^{-1} \quad , \quad PP^{-1}\, = \,PP^{T}\,=\,I $$
$$ \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \,=\, \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
치환 행렬 P는 행렬을 뒤섞는 역할을 한다면, \(P^{T}\)는 원래대로 돌려주는 역할을 한다. 따라서 전치 행렬이 역행렬과 같다.
소거 행렬 E의 경우도 간단하게 생각하면 편하는데, 어떤 값을 빼는 행렬을 원래대로 돌리려면 그 값을 다시 더해주는 행렬을 사용하면 된다.
$$ \begin{bmatrix} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \,=\, \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
다음의 경우도 마찬가지 이다.
$$ \begin{bmatrix} 1 & 0 & 0 \\ -m& 1 & 0 \\ km - l & -k & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ m & 1 & 0 \\ l - km & k & 1 \end{bmatrix} \,=\, \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} $$
LU분해
LU분해는 선형대수에서 가장 대표적인 분해 중 하나이다.
행렬 \(A\)에서 소거법을 통해 상삼각행렬 \(U\)를 얻는다. 이를 식으로 표현하면 다음과 같다.
$$ EA\, = \,U $$
구체적으로 A가 3 by 3 행렬이라면 다음과 같다.
$$ (E_{32}E_{31}E_{21})A\, = \,U $$
여기서 소거 행렬 E는 역행렬이 항상 존재한다. 따라서 각 항에 \(E^{-1}\)를 곱해주면 다음과 같다.
$$ A\, = \,(E_{21}^{-1}E_{31}^{-1}E_{32}^{-1})U $$
주의할 점은 행렬 곱의 역행렬은 항상 역순(reverse order)으로 나타난다는 것이다.
여기서 소거행렬의 역행렬을 보게 되면 대각 행렬의 아래 부분만 원소가 존재한다. 따라서 우측 항은 하삼각행렬과 상삼각행렬의 곱으로 이루어진다. (소거행렬의 역행렬 과정을 보면 쉽게 확인할 수 있다.)
\begin{align} &EA\, =\, U \\ &A\, = \, LU \end{align}

그림 3. LU분해 예시
LDU 분해
LU 분해에서 한 단계 더 나아가면, L(하삼각행렬)의 경우 대각 원소가 모두 1이지만,
U(상삼각행렬)의 경우 대각 원소가 일반적인 값이다.
따라서 LU 분해에서 대각 원소를 분리하여, LDU 분해로 나타낼 수도 있다.
- L: 대각 원소가 1인 하삼각행렬
- D: 대각행렬 (U의 대각 원소를 모은 행렬)
- U: 대각 원소가 1인 상삼각행렬
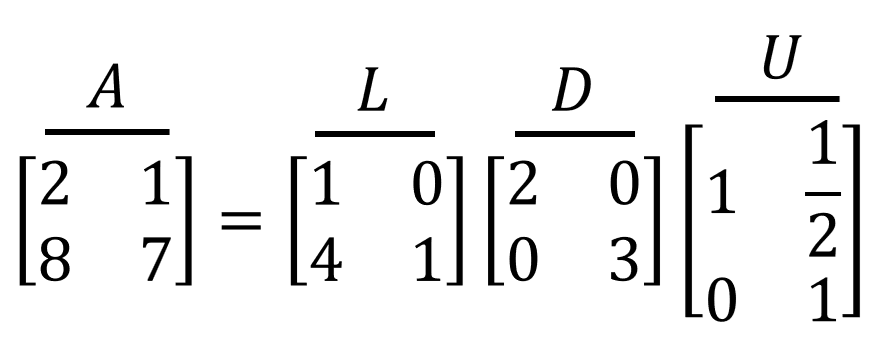
그림 4. LDU분해 예시
참고 자료
- Gilbert Strang, MIT 18.06 Linear Algebra, MIT OCW 강의 (2011)
