2.Elimination(소거법)
Published:
소거법
우리의 목표는 \(Ax=b\)에서 \(x\)를 구하는 것, 즉 linear equation을 푸는 것이다. 이때 사용되는 방법이 elimination(소거법)이다.
소거법을 사용하게 되면,행렬 \(A\)가 상삼각행렬(Upper triangular matrix) \(U\)의 형태로 바꾼다.
그 후 \(Ux= c\)를 풀어 \(x\)를 구할것이다. 예시를 통해 알아보자.
$$ A = \begin{bmatrix}1 & 2& 1 \\3 & 8 & 1 \\ 0 &4 &1 \end{bmatrix}\quad \text{and} \quad b = \begin{bmatrix}2 \\ 12 \\2 \end{bmatrix} $$
Upper triangular matrix란 대각선에 있는 원소 아래쪽이 0인 행렬을 말한다.
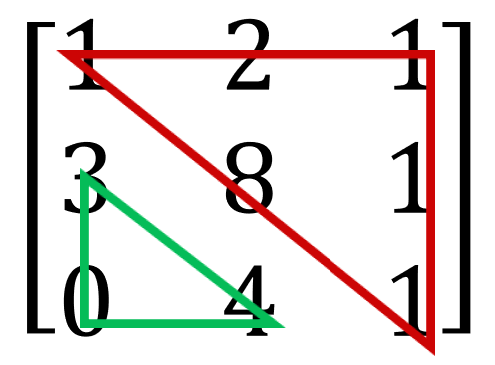
그림 1. Upper triangle
상삼각행렬로 만들기 위해서는 A에서 행들간의 연산이 필요하다.
- 두 번째 행에 첫 번째 행을 3 곱해 빼, 2행 1열의 3을 0으로 만든다.
- 3행 1열의 경우 이미 0이므로 추가 연산이 필요 없다.
- 세 번째 행에 바뀐 두 번째 행을 2 곱해 빼, 3행 2열을 0으로 만든다.
계산 과정의 편의성을 위해 위와 같이 위에서 아래로 차근 차근 계산을 진행한다. 이를 그림으로 보면 다음과 같다.
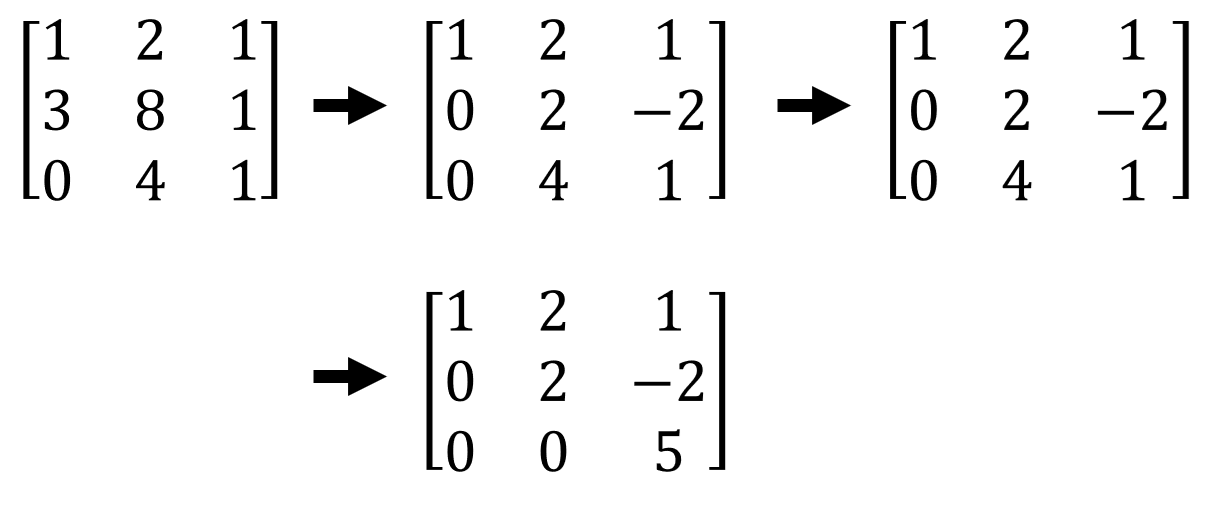
그림 2. 계산 과정
우리는 \(Ax=b\)를 풀고있다. 따라서 왼쪽항에서 계산이 이루어 졌다면 오른쪽 항에서도 계산이 이루어져야 한다. 따라서 행연산이 \(b\)에서도 적용이 되야 하고, \(Ax = b\)가 \(Ux = c\)가 된다.
$$ \begin{bmatrix}1 & 2& 1 \\3 & 8 & 1 \\ 0 &4 &1 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3} \end{bmatrix} = \begin{bmatrix}2 \\ 12 \\2 \end{bmatrix} \Rightarrow \begin{bmatrix}1 & 2& 1 \\0 & 2 & -2 \\ 0 &0 &5 \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3} \end{bmatrix} = \begin{bmatrix}2 \\ 6 \\-10 \end{bmatrix} $$
\(x\)의 경우 간단하게 후방대입법(back substitution)을 통하여 구할 수 있다.
- 마지막 행으로 부터 \(x_{3} = -2\)라는 것을 알 수 있다.
- 두 번째 행에서 \(x_{3} = -2\)을 대입 해 \(x_{2} = 1\)를 구할 수 있다.
- 첫 번째 행에서 \(x_{3} = -2, x_{2} = 1\)를 대입 해 \(x_{1} = 2\)를 구할 수 있다.
결론은 소거법을 통해 상삼각행렬로 만들 수 있다면, 후방대입법을 통해 간단하게 방정식을 풀수 있다.
Pivot과 답을 구할수 없는 경우
후방대입법을 해보면, 상삼각행렬에서 각행의 0이 아닌 첫 번째 원소들이 중요한 역할을 한다고 느낄수 있다. 이 요소들은 pivot이라고 불린다. 정확히는, 행 사다리꼴(row echelon form)에서 각 행의 가장 왼쪽에 위치한 0이 아닌 원소를 pivot이라고 한다.
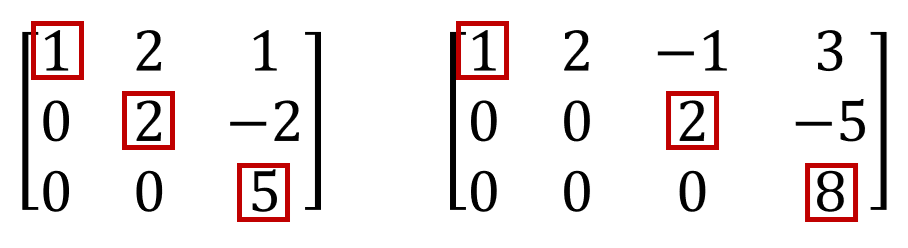
그림 3. Pivot
행 사다리꼴은 별도의 엄밀한 정의가 있지만, 소거법을 진행하면 얻는 상삼각행렬과 비슷한 형태로 이해해도 무방하다.
그림3에서 왼쪽사진의 경우는 후방대입법으로 답을 구 할 수 있다. 하지만 오른쪽의 경우는 답을 구할 수 없다. 답을 구할수 없는 경우와 있는 경우를 정리해보자.
첫 번째는 pivot이 0인경우이다.
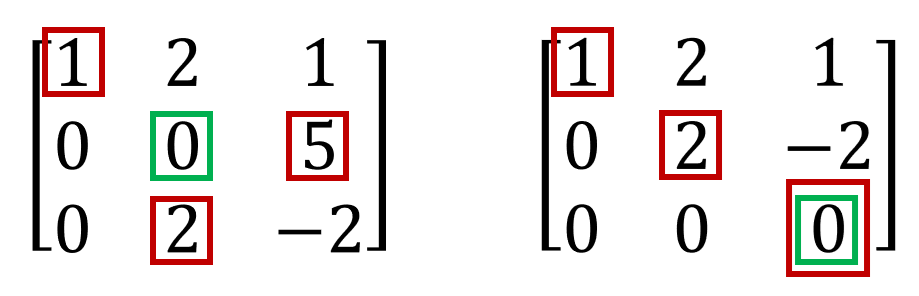
그림 4. Pivot2
정확하게 말하자면 후방대입법으로 답을 구하기 위한 pivot(대각 성분)의 값이 0인 경우이다. 그림4의 왼쪽의 경우는 후방 대입법으로 값을 구할 수 없다. 하지만 두 번째 행렬과 세 번째 행렬 위치를 바꾸면 상삼각행렬이 만들어진다.
즉, pivot 값이 0이더라도 간단한 행 교환으로 0이 아닌 값을 놓을 수 있다면 해가 존재한다.
반면, 그림 4 오른쪽처럼 행 교환으로도 대각 성분에 0이 아닌 값을 놓을 수 없는 경우에는 해가 존재하지 않는다.
pivot은 각 행에서 가장 왼쪽에 위치한 0이 아닌 원소이지만, 여기서는 후방대입법에서 해를 결정하는 대각선 성분의 위치라는 표현으로 이해하면 편할것 같다.
오른쪽 그림의 마지막 행은 모든 원소가 0이다.
이는 \(Ux = c\)에서 마지막 행이 \(0 = 0\) 또는 \(0 = c\) 꼴이 될 수 있음을 의미한다.
- \(0 = c\) (단, \(c \neq 0\)) → 모순이므로 해가 존재하지 않는다.
- \(0 = 0\) » 자유 변수가 생겨 해가 무한히 많다(유일한 해 없음).
이 경우 마지막 행은 이전 행들의 선형 결합으로 표현될 수 있으므로, 행렬은 선형종속(linearly dependent)이다.
선형종속인 행렬은 역행렬이 존재하지 않는 비가역(not invertible), 즉 특이(singular) 행렬이다. (역행렬 부분에서 자세히 설명)
not-invertible행렬이 답을 구 할수 없다는 것을 알았다. 반대로 답을 구할수 있는경우는 n x n 정사각행렬이고, 행렬속 pivot의 개수가 n개인경우 답을 구할수 있다. (pivot의 위치가 대각요소가 아니더라도 행교환을 통해 구할수 있는것을 보였다.) 이러한 경우를 invertible(가역행렬)이라고 한다. pivot의 개수가 n개라는 것은 랭크(rank)가 n이라는 것이고 이는 행렬이 full rank라는 것을 의미한다. 이 또한 뒤에서 나올 것이다.
참고 자료
- Gilbert Strang, MIT 18.06 Linear Algebra, MIT OCW 강의 (2011)
