1.Linear Algebra
Published:
Linear Algebra(선형 대수학)이란
나의 경우 처음 선형대수학 행렬과 벡터를 다루는 방법을 배운다고 생각을 했었다. 막연하게 공부를 하면 능숙하게 다루겠다고 느끼고 공부를 시작했다. 틀린말은 아니지만, 지금 시점에서 내가 느낀 선형대수학은 선형 방정식 \(Ax = b\)를 푸는 방법을 배우는 과목이라고 생각한다.
조금 더 자세히 말하자면, 어떤 1차 방정식(\(x + 2y + z = 3\))이나 행렬, 함수등이 선형성(linearity)을 가진다면 \(Ax = b\)형태로 보고 이를 푸는 방법을 배운다고 생각한다.
함수 \(f\)에 대하여
- 가산성(Additivity), 즉, 임의의 수 \(x, y\)에 대해 \(f(x+y) = f(x) + f(y)\)가 항상 성립하고
- 동차성(Homogeneity), 즉, 임의의수 \(x\)와 \(\alpha\)에 대해 \(f(\alpha x) = \alpha f(x)\)가 항상 성립할 때
함수 \(f\)는 선형이라고 한다.(wikipia)
지금 까지 배운 거의 모든 부분이 선형 방정식(1차 방정식)을 푸는 방법이기 때문에 이에 관한 이야기를 하겠다.
선형 방정식을 다루는 방법에는 3가지의 관점이 있다. 다음 예시를 통해 알아보자.
$$ \begin{aligned} 2x - y &= 0 \quad \text{...(1)} \\ -x + 2y &= 3 \quad \text{...(2)} \end{aligned} $$
간단하게 행과 열의 개념을 잡자면, 행은 가로줄을 뜻하고 열은 세로줄을 의미한다.
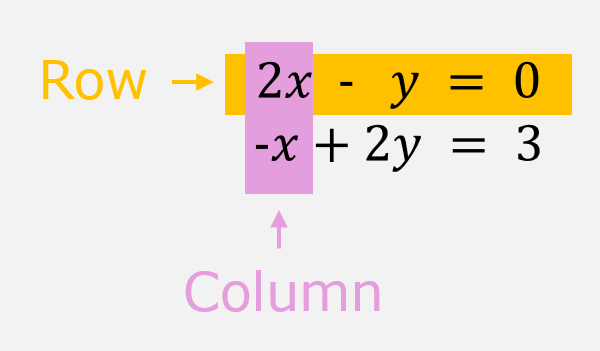
그림 1. 행과 열을 읽는 방법
Row picture
가장 먼저 row picture의 경우는 일차 방정식으로 문제를 해석한다. 예시는 \(x\),\(y\) 2개의 미지수로 이루어진 일차방정식이다.
일차 방정식이므로 각각은 직선을 나타내며, 해는 이 직선들의 교점이 된다.
이러한 해를 구하는 방식은 고등학교에서 배운, n개의 미지수에 대해 n개의 방정식을 이용하는 해법과 같다.
예시의 교점은 (2,1)로 다음과 같다.
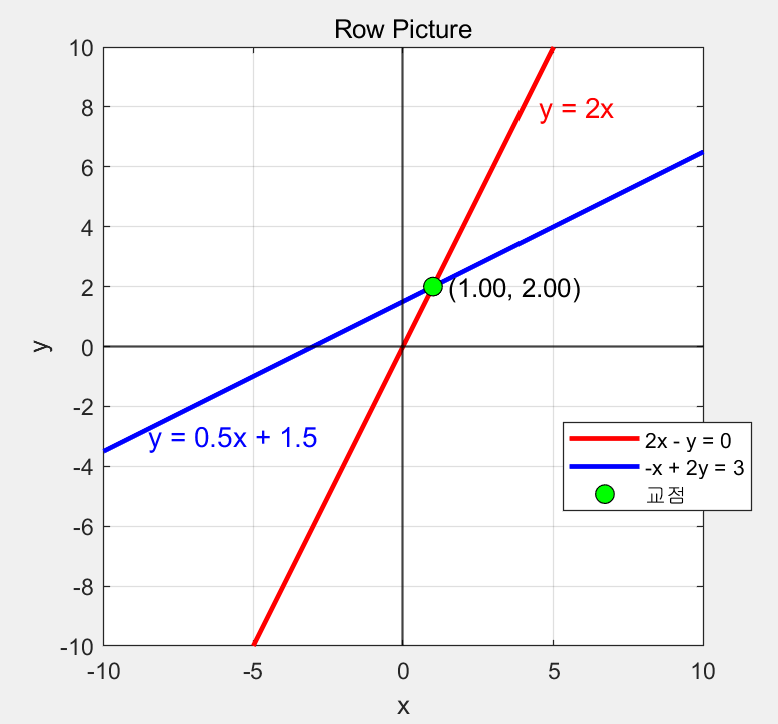
그림 2. 두 직선을 나타낸 Row picture
Column picture
다음으로는 column picture의 경우는 방정식을 vector로 문제를 바라본다. 정확하게는 미지수 앞의 계수들을 벡터로 보고, 미지수를 상수로 보아 벡터들 간의 선형결합으로 문제를 바라본다.
$$ \begin{bmatrix}2 \\-1 \end{bmatrix}x + \begin{bmatrix}-1 \\2 \end{bmatrix}y = \begin{bmatrix}0 \\3 \end{bmatrix} \quad \text{...(3)} $$
이런식으로 column vector로 문제를 바라본다. 벡터를 배울 때는 row vector와 column vector 두 가지로 배웠지만, 선형대수학에서는 보통 “벡터”라고 하면 column vector(열 벡터)를 의미한다.
행 벡터는 보통 전치(transpose) 기호인 \(A^{T}\)를 통해 표시하고, 열 벡터를 간단히 나타내기 어려울 때는 (2, -1)처럼 소괄호를 사용하기도 한다.
선형결합이란, 벡터(각 항)에 상수를 곱하고 결과를 더해 만든 표현식을 말한다. 예를 들어 벡터 \(x,y\)가 있을 때, \(x\)와 \(y\)의 선형결합은 \(ax + by\)이다.
여기서 a와 b는 상수인데, 식3에서는 \(x\)와 \(y\)는 일차식의 미지수로 상수의 역할을 한다. 따라서 column picture는 벡터들의 선형결합으로써 문제를 바라본다.
결론적으로는 식3의 오른쪽 벡터를 왼쪽 벡터들의 선형결합을 통해 구해야 한다. 예시의 경우는 각 벡터의 2배, -1배 해서 더하면 오른쪽의 \((0,3)\)이 된다.
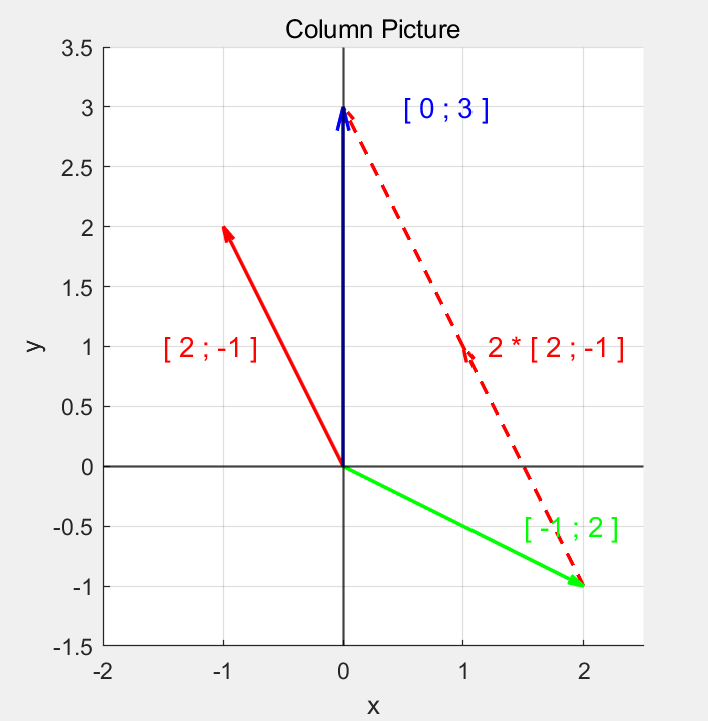
그림 3. 벡터들간의 선형결합으로 바라보는 column picture
Matrix picture
마지막으로 matrix picture의 경우는 column picture에서 더 나아가서 column vector들을 행렬로 바라보고, 행렬과 벡터의 곱으로써 바라보는 방법이다.
$$ \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} \quad \text{...(4)} $$
다음과 같이 미지수를 벡터로 보고 열 벡터를 모아서 행렬로 바라보는 방식이다. 이와 같은 방법을 통해 행렬 A와 벡터 x 그리고 오른쪽 벡터 b로써 \(Ax=b\)의 형태로 여러개의 선형 방정식을 하나의 선형 방정식으로 생각할수 있게 된다.(앞에서 말한 선형 대수학이 \(Ax=b\)를 푸는 방법을 배운다고 한 이유)
마치며
row picture는 매우 친숙한 교점을 구하는 방법이라고 생각한다. 하지만 column picture에 익숙해지면 문제 풀기도 쉽고, 머릿속에 문제를 그리기도 편하다고 생각한다.
교점을 구하는 방식은 2차원에서는 익숙하고 직관적일 수 있지만, 3차원이나 n차원으로 넘어가면 시각적으로 교점을 파악하기 어려워진다. 하지만 벡터의 관점으로 보면 결국 벡터들간의 선형결합으로써 정답을 구하기 때문에 머릿속에 그리기 편하다고 생각한다.
Gilbert Strang 교수는 column picture에 익숙해지는 것을 권장한다.
실제로 n차원 공간에서는 교점보다는 벡터의 선형 결합을 통해 해를 직관적으로 이해하는 것이 더 유리할 수 있다.
참고 자료
Gilbert Strang, MIT 18.06 Linear Algebra, MIT OCW 강의 (2011)
